神经网络，决策树和优化

神经网络（Neural network）

神经网络是模仿人类的神经元来设计的，虽然我们对人类大脑的具体原理还不清楚，但模仿神经元设计的神经网络的功能是非常强大的。

结构

神经网络的结构是层级的，每一层（Layer）包含一个或多个神经元（Neuron）。每一个神经元都有自己的参数（\(w\),\(b\) ）,从前一层获取值并经过自己的参数计算，传递给激活函数（Activation function），最终输出一个激活值。每层的所有神经元的激活值合并到一起就构成了这一层的输出。图例为两层的神经网络，第一层有三个神经元，第二层为输出层，有一个神经元。

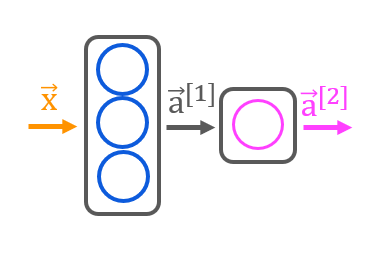
神经网络模型模型的输入会从左到右通过所有的层，得到一个输出，即神经网络的推断结果。这一过程也成为前向传播（Forward propagation）

代码表示

使用目前比较流行的 Tensorflow 库来构建神经网络。代码示例：

import tensorflow as tf
import numpy as np
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras.activations import linear, relu, sigmoid

X_train
y_train 
# 构建模型
model = Sequential(
    [
        Dense(3, activation = 'relu',   name = "L1"),
        Dense(1, activation = 'linear', name = "L2")
    ]
)

# 指定损失函数和优化方式
model.compile(
    loss=tf.keras.losses.BinaryCrossentropy(from_logits=True),
    optimizer=tf.keras.optimizers.Adam(0.001),
)

# 训练模型
model.fit(
    X_train,y_train,
    epochs=200
)

# 使用训练好的模型来预测
predictions = model.predict(X_testn)

Sequential 用于指定神经网络模型的架构（有多少层，每层的类型），Dense 是一种层的类型，它可以指定该层的神经元个数，激活函数种类。compile 函数用于指定模型的代价函数和优化器类型。最后调用 fit 函数使用数据训练模型，epochs 用于指定训练数据训练多少次。Tensorflow 会在训练时将训练数据分为 batches 。每个 batch 大小为 32 。

激活函数

目前有三种常用的激活函数：

  • Linear：activation = \( f(x) \)。可以输出正负都很大的值。
  • sigmoid： activation = \( \frac{1}{1+e^{-f(x)}} \)。输出的值的范围在 0 ~ 1 之间。
  • ReLU：activation = \(max(0,f(x)) \)。输出的值大于等于 0 。

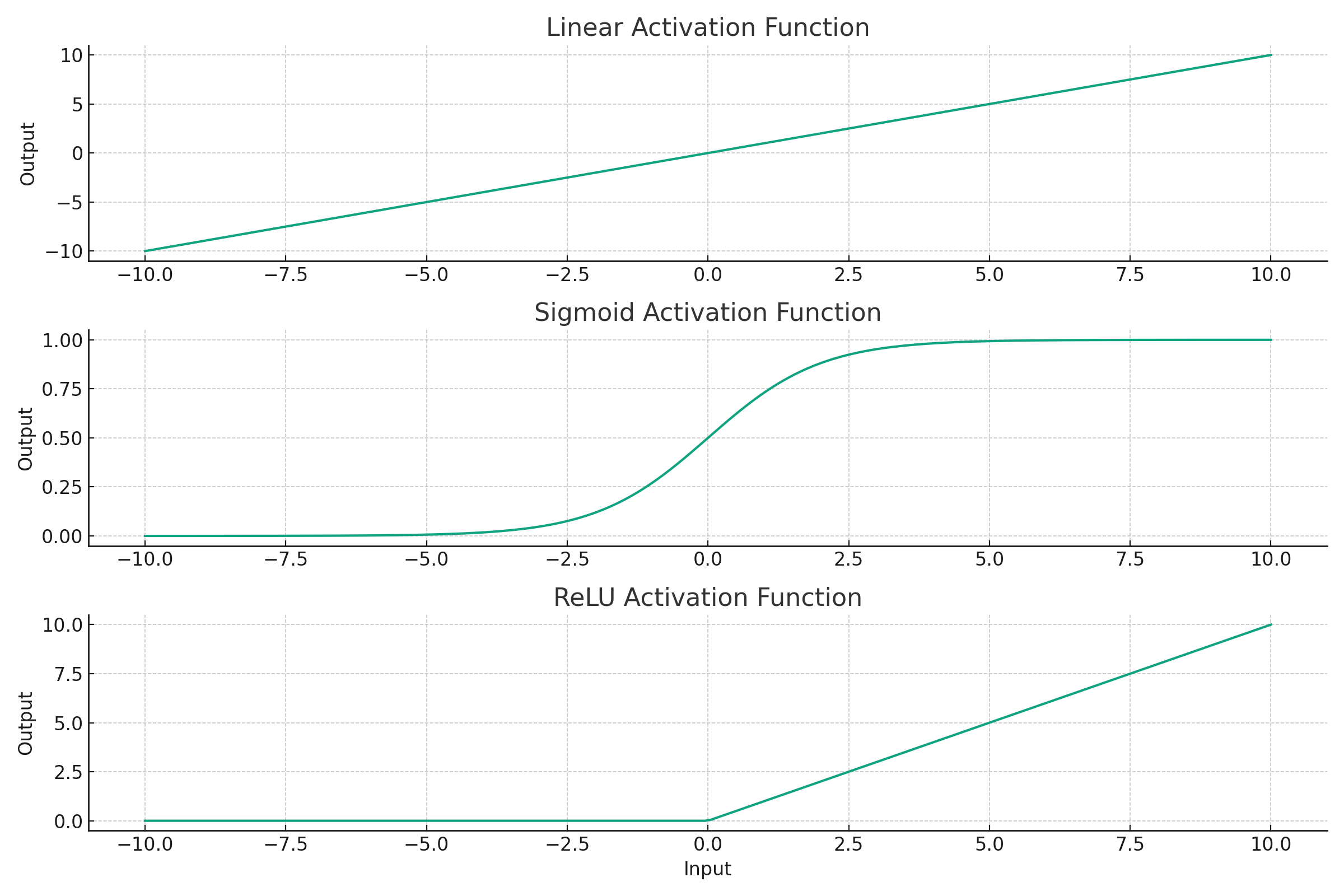
激活函数对比图

一般建议在所有的非输出层，即隐藏层使用 ReLU 激活函数，它相比于 sigmoid 函数计算更快。如果在所有层使用 Linear 激活函数（或者不使用激活函数），则整个神经网络就退化为一个线性回归模型了。

Softmax

softmax 是一种回归的类型，它可以从几个特定的种类中输出一个种类。类似逻辑回归，但逻辑回归只能输出 0 或 1， softmax 的结果可以是很多种类中的一个。借用吴恩达老师课程中的图片：

激活函数对比图

用在神经网络中，最后的输出层输出的结果是一个向量，向量中的每个元素对应结果是该种类的概率值。该向量中值最大的元素的索引就是神经网络最终预测的种类。

代价函数

$$ \mathbf{1}\{y == n\} = =\begin{cases} 1, & \text{if $y==n$}.\\ 0, & \text{otherwise}. \end{cases} $$

$$ J(\mathbf{w},b) = -\frac{1}{m} \left[ \sum_{i=1}^{m} \sum_{j=1}^{N} 1\left\{y^{(i)} == j\right\} \log\frac{e^{z^{(i)}_j}}{\sum_{k=1}^N e^{z^{(i)}_k} } \right] $$

代码表示

model = Sequential(
    [
        Dense(2, activation = 'relu',   name = "L1"),
        Dense(4, activation = 'linear', name = "L2")
    ]
)
model.compile(
    loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True),
    optimizer=tf.keras.optimizers.Adam(0.01)
)

model.fit(
    X_train,y_train,
    epochs=200
)

这样可以构建一个解决多个类别选一个问题的神经网络。最后一层使用 linear 激活函数而不是 softmax，在代价函数中加入 from_logits=True ，这样可以提高训练的精度。

高级优化法

相比于梯度下降，一个更高级的优化方法是 Adam 法，相较于梯度下降，它的学习率 \(\alpha\) 是不固定的，可以在训练过程中根据训练情况实时自动调整，避免学习率过大和过小导致的问题。使用方法很简单，上面的代码已经用到了 Adam 。只需在 compile 函数中指定 optimizer=tf.keras.optimizers.Adam(0.01) 即可。0.01为初始的学习率。

其他类型的层

目前用到的层都是 Dense 层，它的每个神经元都会接受前一层的所有数据作为输入。还有一种叫做卷积（convolutional layer）的层，它的每个神经元接受前一层的特定位置的值作为输入。比如前一层输出了十个数据，这一层的第一个神经元只接收前三个，第二个神经元只接收第四到第六个作为输入。如果神经网络中由多个卷积层，这样的神经网络也叫卷积神经网络。组合多种不同的层可以构成不同的神经网络模型。

反向传播

反向传播是神经网络训练过程的方式，由于神经网络由很多参数，很多层级，单纯的从输入开始计算偏导数到输出的计算量会很大。因为会涉及重复的运算。使用反向传播的方式，从输出开始向输入的方向计算每个参数的偏导数，使用链式法则将偏导数结合起来可以一次遍历计算完所有需要的导数。

模型评估和优化

当模型在实际数据上的预测表现不佳时，有很多可以考虑做的优化方法，例如：收集更多的数据，尝试减少特征的数量，尝试寻找新的特征，尝试增加多项式特征，增大正则化系数，减小正则化系数等。这时候就需要正确评估什么方法是有效的。

模型选择

选择使用什么样的模型来解决问题是很重要的一步，需要从多种模型（多项式，神经网络）中挑选最合适的那个。所以，我们将数据集分为三部分：

  • 训练集（training set），占总数据集的 60%，用于训练模型
  • 交叉验证集（cross validation set），占总数据集的 20%，用于评估各个模型的效果
  • 测试集（test set），占总数据集的 20%，用于测试交叉验证集选出的最优模型的泛化程度

流程为：先构建多个不同的模型，在训练集上将所有模型都训练好，然后计算所有模型在交叉验证集上的代价（cost），挑选出代价最小的那个模型，最后，计算挑选出的模型在测试集上的代价，用这个代价来评估模型的泛化程度。

Bias and Variance tradeoff

评估 Bias 和 Variance 需要一个基准，这个基准可以为：

  • 人类水平
  • 竞争算法的水平
  • 凭借经验的猜测

当模型的表现不佳时，一般分为两种情况，High bias(欠拟合) 或 High variance(过拟合)。两者都有的情况很少见。

  • High bias 表现为在训练集上的准确率和基准相差很大，在交叉验证集上也和基准相差很大。
  • High variance 表现为在训练集上的准确率和基准近似，在交叉验证集上和基准相差很大。

根据这两种情况应该做不同的事情来优化模型：

High bias:

  • 增加多项式特征
  • 尝试增加特征的数量
  • 降低正则化参数大小

High variance:

  • 增加正则化参数大小
  • 尝试减少特征的数量
  • 获取更多训练数据

神经网络被认为是 low bias model 。所以经常要处理的是 high variance 问题。

错误分析（Error analysis）

错误分析（Error analysis）是指查看部分模型输出结果不对的数据，分析这些数据的类型。比如，有一个模型，它的输出结果是十个种类中的一个。查看100个模型输出错误的例子，其中，1个是类型1，20个是类型2，50个是类型3，等等。找到这之中占比比较大的结果来进行优化。在这个例子中就是类型3和类型2，根据这两个结果来优化模型会取得较大的效果。可以尝试多收集一些类型3和类型2的数据。或者调整模型参数（架构，正则化参数等等）。

数据增强（Data argumentation）

数据增强是一种用来生成更多数据的方法。在输入的数据为图像时，可以对图像进行旋转，镜像，缩放，扭曲等操作来生成新的数据。如果输入是声音数据，可以对声音增加不同的背景噪音来生成新的数据。这些生成的新的数据可以让我们的模型训练的更好。

转移学习（Transfer learning）

在神经网络中，一般会存在很多的层，当我们要训练的神经网络的输入和别人训练好的神经网络的输入相同时，比如：都是相同大小的图片。可以直接下载别人训练好的神经网络参数，把这些参数作为我们训练神经网络的初始参数。然后有两种做法：

  • 根据这些初始参数在我们的数据上重新训练所有的参数。
  • 只根据我们的数据训练输出层的参数，其余参数不变。

别人训练好参数的步骤成为监督式预训练（supervised pretraining），我们根据别人训练好的参数来训练我们的模型的过程成为微调（fine tuning）。这种方式可以让我们不需要很多的数据就可以训练出我们自己的模型，还可以减少我们的训练时间。

机器学习项目的完整循环

借用吴恩达老师课程的图片：

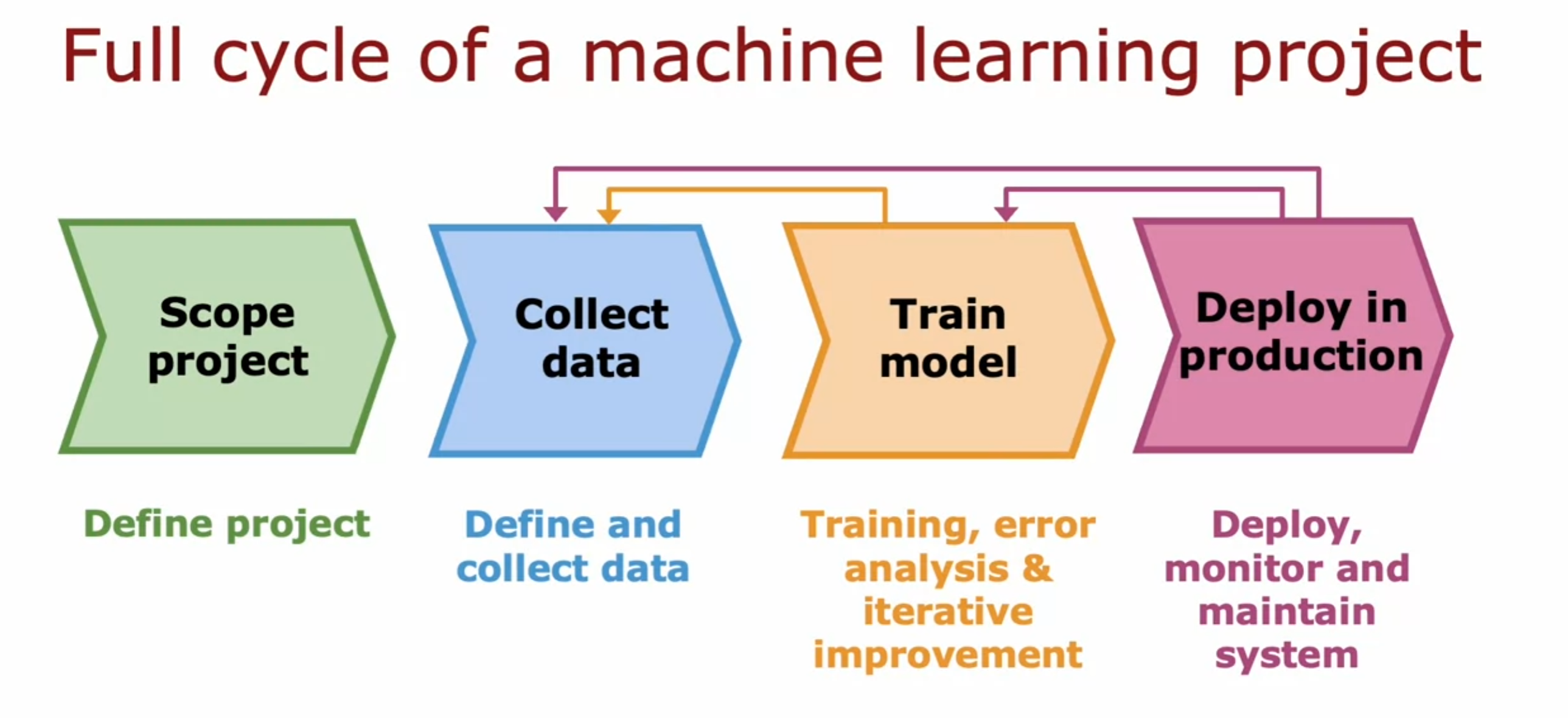
机器学习项目的完整循环

避免歧视，不公，遵循伦理

当机器学习的模型涉及到对人进行评判和根据不同的人觉得不同的结果时，需要额外关注训练好的模型有没有对不同的人有歧视歧视，不公的现象，生成的内容有没有不遵循伦理的现象。目前并没有一些准则可以完全保证遵循了之后可以完全不会出现歧视。所以，在模型的构建过程中对模型进行不同这方面的测试是很有必要的。

偏斜的数据集（Skewed datasets）

有时，我们的数据集在各种结果下的数据占比相差是非常大的。比如有一种很少见的疾病，发病率只有 0.5%。我们的数据集中有 0.5% 是患者。当我们根据这个数据集训练一个模型后，假设模型最后预测错了 1% 的数据，我们可能认为这个模型是一个比较不错的模型。但假设我们有另一个模型，不管数据的数据是什么，它都输出这个样本没有患病。这样，它预测错的比例只有 0.5%！比我们训练的模型还好。显然这个模型是来搞笑的，但它表现的就是很好。所以，我们需要新的方式来评估模型

精确率/召回率（Precision/Recall）

实际（1）实际（0）
预测（1）真阳假阳
预测（0）假阴真阴

精确率 = 真阳 / （真阳 + 假阳）

召回率 = 真阳 / （真阳 + 假阴）

当我们用这两个指标来评估模型时，我们上边一直预测为 0 的模型的这两个指标都会为 0 。我们就知道这个模型是不可用的。

权衡

当我们采用了精确率/召回率来评判我们的模型后，我们可以根据具体的需求来调整判断阈值来让我们的预测更加符合要求。当我们想要增加模型的精确率时，即当我们的模型预测结果为 1 时，我们有很大的信心确定该样本就是阳性结果（比如当一种病的治疗会带来较大代价，而不治疗的代价相比来说更小）。我们可以调大阈值，比如从 0.5 调到 0.8。这样，我们模型的精确率就会增加。相反，当我们想要增加模型的召回率时，即我们想要尽可能的将可疑的样本都预测为阳性（比如当一种病放着不管的代价很大，早发现并治疗的代价很小）。我们可以调小阈值，比如从 0.5 调到 0.2 。这样，我们模型的召回率就会增加。

可以看出，精确率和召回率是一个增大另一个就会减小，所以我们需要权衡它们。简单的将他们平均并不能帮助我们很好的权衡他们，所以我们采用 F1 score 来评估他们。

F1 score 也叫 调和平均数（harmonic mean），具体公式为：

$$ F1 score ={\frac {2}{{\frac {1}{x_{1}}}+{\frac {1}{x_{2}}}}}={\frac {2x_{1}x_{2}}{x_{1}+x_{2}}} $$

调和平均数更关注数据中更小的项，当两个数据中一个很小时，它的调和平均数是比两个差不多的数据的调和平均数小的。所以，我们选择 F1 score 比较大的模型就可以得到更均衡的模型。

决策树（Decision tree）

决策树是一种用来分类的模型，它可以从数据集中学习，根据数据集的特征来将数据集划分为几个子集。具体的过程为：

  1. 在数据集上使用尝试所有特征来进行数据集的划分
  2. 计算所有划分后的信息增益
  3. 选取最大信息增益的特征作为划分的依据，在划分好的子集中重复以上步骤直至满足结束条件

信息增益（Information gain）

信息增益的计算公式为：

$$ \text{Information Gain} = H(p_1^\text{node})- \left(w^{\text{left}}H\left(p_1^\text{left}\right) + w^{\text{right}}H\left(p_1^\text{right}\right)\right), $$

\(H\) 是熵, 公式为：

$$ H(p_1) = -p_1 \text{log}_2(p_1) - (1- p_1) \text{log}_2(1- p_1) $$

\(p\) 是单个节点的纯度，是一个分数，分子为满足条件的数据数量，分母为该集合中所有数据的数量。

结束条件

结束条件有很多选择：

  • 当一个节点全部都属于一个种类
  • 当树的深度达到设定的最大值
  • 继续划分的信息增益小于设定的阈值

one-hot encoding

有时我们数据的特征不只是有或没有，而是好几个选项中的一个。这时，我们需要将这个特征进行 one hot encoding。

例： 有一个特征为皮肤颜色，它可以是黑色，白色，黄色。我们需要将这个特征分为三个特征：是否黑色皮肤，是否白色皮肤，是否黄色皮肤。这样就可以满足决策树的特征划分要求。

连续值特征处理

当一个特征为连续的值时，比如体重。我们需要将这个特征分别按照几个阈值进行划分，计算每次划分前和后熵的差值，选取差值最大的那个作为阈值。当该特征的值小于这个阈值时将这个值转换为 0 ，大于则转换为 1 。

阈值可以按照划分数据集的权重来从头尝试到尾。比如有十个数据，将它从小到大排序，一开始将最小的那个划分到左边，剩下九个划分到右边，计算熵的差值。然后将最小的两个划分到左边，剩下八个划分到右边。。。。。。

回归树

相较于分类的决策树，回归树的输出值不是特定的。它可以输出连续的值。它在划分子集的时候用到的依据不是熵减的大小，而是方差的大小。没每次选取方差减小的最大的那个特征作为划分依据。最后输出的结果是该子集中所有数据的平均值。

Tree Ensembles

单个决策树对数据中的微小变化很敏感，为了提高模型的鲁棒性我们可以训练很多个决策树，我们可以称这些决策树为一个 tree ensemble。我们最终的结果是这个 tree ensemble 中的所有树的输出中最多的那个。为了构建这样的树，我们需要用到有放回的抽样（Sampling with replacement）。假设总共有 10 个数据，我们可以在这个 10 个数据上使用有放回抽样 3 次，这样我们就会得到三组额外的数据，可以在这三组数据上训练出三个不同的决策树。

Random forest algorithm

随机森林算法（Random forest algorithm）会使用上边说到的有放回抽样，重复 B 次。假设我们有 n 个特征，当每个节点要选取特征作为划分的依据时，它不会从所有的特征中选择，而是从一个具有 k (k < n) 个特征的随机子集中选择信息增益最大的那个特征。k 一般取 n 的平方根。

XGBOOST(eXtreme Gradient Boosting)

XGBOOST 是一种更强的决策树模型，相较于普通的决策树，它每次有放回抽样时会优先考虑之前的决策树分类错误的样本，也就是刻意练习。这会让我们的模型训练的效果更好。它也包含了正则化来防止过拟合。代码示例为：

# Classification
from xgboost import XGBClassifier

model = XGBClassifier()

model.fit(x_train, y_train)
y_pred = model.predict(X_test)

# Regression
from xgboost import XGBRegressor

model = XGBRegressor()

model.fit(x_train, y_train)
y_pred = model.predict(X_test)

神经网络和决策树的抉择

决策树

当我们的数据时结构化的数据，比如数字，种类等。我们可以考虑使用决策树。相较于神经网络模型，决策树的训练会更快速，较小的决策树叶更容易人类理解。

神经网络

当我们的数据是非结构化的数据，比如图片，语言等，我们需要使用神经网络来构建模型，当然，神经网络模型也可以根据结构化的数据构建，它在这两种数据上的效果都很好。但神经网络相较于决策树会训练的慢一些，导致我们迭代模型的速度也会较慢。不过神经网络可以借助 transfer learning 来更快更好的训练。当我们需要构建一个多模型共同运行的系统时，神经网络模型相较于决策树更容易整合。